Algorytm Euklidesa

Poniższy materiał to część cyklu „Algorytmy dla uczniów”

Algorytm Euklidesa czyli algorytm wyznaczania  NWD – największego wspólnego dzielnika dwóch liczb całkowitych.

Na początku wykonajmy proste zadanie.

Zadanie:
Wyznacz największy wspólny dzielnik dwóch liczb naturalnych: 12 , 18.

Na początku wypiszmy wszystkie dzielniki dla każdej z liczb:

12 – 1, 2, 3, 4, 6, 12
18 – 1, 2, 3, 6, 9, 18
wspólne dzielniki: 1, 2, 3, 6
największy wspólny dzielnik: 6

Teraz wybierzmy wspólne dzielniki tych liczb. Będą to liczby 1, 2, 3, 6.
Zatem największym wspólnym dzielnikiem jest liczba 6. Zapiszmy: 
NWD(12, 18) = 6

Zadanie:
Napisz algorytm wyznaczania NWD(a, b)

Na tym etapie możemy zastanowić jak wyznaczyliśmy wspólny dzielnik i opracować algorytm. Ale … możemy po prostu skorzystać z gotowego rozwiązania, które opracował Euklides.

Algorytm Euklidesa

Wyznaczanie NWD, a więc największego wspólnego dzielnika dwóch liczb naturalnych zrealizujemy za pomocą algorytmu Euklidesa.

Algorytm Euklidesa z wykorzystaniem odejmowania

Algorytm ten  opiera się on na spostrzeżeniu, że jeśli odejmiemy od większej liczby mniejszą, to ta mniejsza liczba i otrzymana różnica będą miały taki sam największy wspólny dzielnik jak pierwotne liczby. Jeśli w wyniku kolejnego odejmowania otrzymamy parę równych liczb, oznacza to, że znaleźliśmy NWD.

Poszukajmy zatem NWD metodą Euklidesa:

        a   |   b
        12 | 18
        12 | 18-12= 6
12-6= 6 | 6

Skąd wzięły się te obliczenia? Spójrzmy powyżej. Na początku mamy dwie liczby 12 i 18, które dla ułatwienia umieściliśmy sobie w kolumnie a i kolumnie b. Sprawdzamy czy liczby są równe. Nie są, 12 nie jest równe 18. Zatem przystępujemy do obliczeń. Sprawdzamy , która liczba jest większa i od niej odejmujemy mniejszą.  Zatem odejmujemy od liczby b liczbę a (bo 18 jest większe od 12). Zapisujemy  18-12 i otrzymujemy wynik 6 . W kolumnie a przepisujemy liczbę, która była powyżej czyli 12. 
I teraz znowu sprawdzamy wyniki, które uzyskaliśmy. Czy a=b?, nie, bo 12 nie jest równe 6. Wybieramy kolumnę z większą wartością,  u nas będzie to kolumna a , bo 12>6. I znowu odejmujemy od większej liczby mniejszą. Zatem w kolumnie a: od 12 odejmujemy 6 i zapisujemy wynik 6. Wartość w kolumnie b przepisujemy, czyli wpisujemy 6, tak jak było wiersz wyżej.
I znowu sprawdzamy czy a=b, tym razem warunek jest prawdziwy, liczby są równe, bo 6=6. Zatem kończymy algorytm i wypisujemy wynik z kolumny a, czyli liczbę 6.

Przestawimy teraz algorytm Euklidesa za pomocą pseudokodu, schematu blokowego oraz języka C++.

Pseudokod:

dopóki a!=b wykonuj
  jeśli a>b to a=a-b
   w przeciwnym przypadku b=b-a
wypisz a

Algorytm Euklidesa: schemat blokowy

Przedstawimy teraz algorytm w postaci schematu blokowego. Na początku następuje wczytanie dwóch liczb. Następnie sprawdzamy czy są to takie same liczby. Jeśli bowiem liczby są równe to od razu wiemy iż ich wspólnym dzielnikiem jest ta sama liczba.
Jeśli liczby są różne sprawdzamy, która z nich jest większa, by od większej liczby odjąć mniejszą.

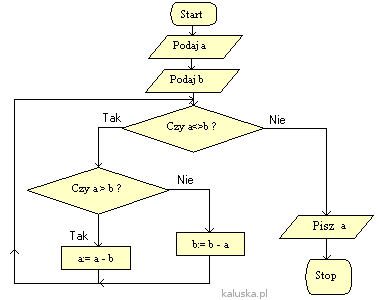Algorytm Euklidesa. Schemat blokowy

Algorytm Euklidesa w języku C++

Funkcja nwd ma postać:

int nwd(int a, int b){
 while (a!=b){
 if (a>b)
 a=a-b;
else
 b=b-a;
 }
return a;
}

Należy zauważyć, że w przypadku gdy różnica między liczbami a i b jest znacząca, to odejmowanie będzie wykonywane dużą liczbę razy. Dlatego w drugiej wersji odejmowanie zastąpione zostało wyznaczaniem reszty z dzielenia.

Algorytm Euklidesa z wykorzystaniem dzielenia

Podany wyżej algorytm można zmodyfikować zastępując odejmowanie resztą z dzielenia większej liczby przez mniejszą.

Przeanalizujmy ponownie przykład poszukiwania NWD(25,35):

              a  |    b 
           25   |    35      
           25   | 35%25=10
25%10=5  | 10
             5   | 10%5=0

Obliczenia kończymy, gdy jedna z liczb przyjmuje wartość 0. W naszym przykładzie NWD(25,35)=5.

Algorytm można uprościć przyjmując, że a będzie zawsze wartością większą od b.

Pseudokod:

dopóki b!=0 wykonuj
    pom←b
    b←a mod b
    a←pom
wypisz a

Podsumowanie

Ten artykuł jest częścią cyklu „Algorytmy dla uczniów”. Cały kurs zawierający materiały dotyczące algorytmów dla początkujących zawiera:

Lekcja 1: Co to jest algorytm? Podstawy algorytmów

Lekcja 2:  Sposoby zapisu algorytmów

Lekcja 3: Rodzaje algorytmów

Lekcja 4: Schematy blokowe algorytmów

Lekcja 5: Specyfikacja algorytmu. Specyfikacja problemu algorytmicznego

Lekcja 6: Algorytmy Przykłady i zadania 

Lekcja 6.1: Algorytmy. Przykłady i zadania.  Obliczanie pola trójkąta

Lekcja 6.2:  Algorytmy. Przykłady. Algorytm Euklidesa

Lekcja 6.3: Algorytm. Gra Kamień Papier Nożyce

Lekcja 7. Przykłady schematów blokowych. Ciągi liczb

Lekcja 8. Sortowanie – algorytmy sortowania

Lekcja 9: Algorytmy. Tablice jednowymiarowe

Lekcja 10. Algorytmy. Tablice dwuwymiarowe