KALUSKA

Wpisy, których autorem jest kaluska.pl

kaluska.pl
28 posts

Oracle. Darmowa baza danych do nauki

Bazy danych
0
Darmowa baza danych Oracle: instalacja i nauka Darmowa baza  danych Oracle Czy istnieje jakaś darmowa wersja bazy Oracle, którą można pobrać i używać do nauki? Tak, jak najbardziej Pobieranie plików Możemy skorzystać chociażby z udostępnionej przez Oracle wersji: Oracle Database Express Edition 11g Release 2 Pamiętajmy również by pobrać Oracle SQL Developer.…

Co to jest algorytm. Podstawy algorytmów

Algorytmy
0
Blog o programowaniu
CO TO JEST ALGORYTM ? Na lekcjach matematyki czy fizyki często słyszymy zdanie „rozwiąż zadanie”. Większość tych zadań rozwiązujemy według pewnych schematów. Najpierw wypisujemy dane i zastanawiamy się do jakiego celu dążymy, a więc jaki ma być wynik. Następnie wypisujemy wzory łączące dane z szukanymi bądź twierdzenia, które można zastosować.…

Schematy blokowe algorytmów

Algorytmy
0
Blog o programowaniu
Do tej pory do opisu algorytmów używaliśmy języka potocznego. Były to jednak algorytmy proste, które ma wykonywać człowiek. W przypadku algorytmów skomplikowanych ten zapis będzie nieczytelny, nie sprawdzi się. Dlatego teraz poznamy nowy, bardziej przejrzysty sposób – schematy blokowe. Schemat blokowy to graficzny zapis sposobu rozwiązania zadania, przedstawiający opis i…

Algorytmy: ciągi liczb. Schematy blokowe algorytmów

Algorytmy
0
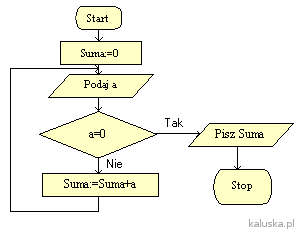
Algorytmika: przykłady algorytmów
Ciągi w algorytmach. Przykłady schematów blokowych Przykład 1 Dany jest ciąg liczb o nieznanej długości. Ostatnia liczba w ciągu równa się zero. Oblicz sumę elementów tego ciągu. Schemat blokowy algorytmu Przykład 2 Oblicz sumę n – kolejnych liczb naturalnych. Pierwsza z liczb wprowadzona z klawiatury i równa się b. Przykład…

Algorytmy sortowania

Algorytmy
0
Blog o programowaniu
ALGORYTMY SORTOWANIA (PORZĄDKOWANIA) Sortowanie (porządkowanie) – proces ustawienia zbioru obiektów w określonym porządku Metody sortowania: przez zamianę (sortowanie bąbelkowe) przez wybieranie przez wstawianie ALGORYTM SORTOWANIA BĄBELKOWEGO Jedną z popularnych metod sortowania jest sortowanie przez prostą zamianę (sortowanie bąbelkowe). W metodzie tej porównujemy sąsiednie elementy. W celu uporządkowania elementów od najmniejszego…

Algorytm. Gra Papier Kamień Nożyce

Algorytmy
0
Algorytmika: przykłady algorytmów
Grę „Papier Kamień Nożyce” znają chyba wszyscy. Tym razem naszym zadaniem jest stworzenie algorytmu wskazującego zwycięzcę tej gry. Zakładamy, że w grze uczestniczą dwaj gracze. Każdy z graczy może wybrać (pokazać) jedną z trzech wartości: papier albo kamień albo nożyce. Możemy więc przystąpić do tworzenia specyfikacji algorytmu: Dane wejściowe: g1:…

Algorytm. Obliczanie pola trójkąta

Algorytmy
0
Blog o programowaniu
Stworzymy algorytm obliczający pole trójkąta. Rozpoczniemy od zapisania specyfikacji problemu. Specyfikacja algorytmu obliczającego pole trójkąta Problem: Obliczanie pola trójkąta. Dane: a, b, c – trzy dowolne liczby Wynik: Jeśli liczby a, b, c są długościami boków trójkąta to wyznaczamy S – pole tego trójkąta. Jeśli liczby a,b,c nie tworzą trójkąta wyprowadź komunikat,…

Algorytmy. Tablice jednowymiarowe

Algorytmy
0
Blog o programowaniu
  ALGORYTMY OBSŁUGI TABLIC Tablicą nazywamy złożoną strukturę danych, która zawiera zbiór elementów tego samego typu.Wyróżniamy: tablice jednowymiarowe tablice wielowymiarowe TABLICE JEDNOWYMIAROWE Tablica jest to zbiór elementów tego samego typu. Każdy element tablicy jest identyfikowany przez jego numer (indeks). Każdy element tablicy posiada swoją wartość. Oto tablica o nazwie „t”…

PL/SQL. Rodzaje bloków

Bazy danych
0
WSTĘP DO PL/SQL Rodzaje bloków PL/SQL: 1. bloki anomimowe (nienazwane) declared inline 2. bloki nazwane (podprogramy) Blok anonimowy Uruchamiamy program Oracle SQL Developer. Wpisujemy poniższy kod: BEGINDBMS_OUTPUT.PUT_LINE(‚Hello World!’);END; By wykonać kod wciskamy przycisk Run Script (zielona strzałka z kartką) lub wciskamy klawisz F5. Zobaczymy informację: PL/SQL procedure successfully completed. Aby wyświetlić…

SQL. Pobieranie danych z kilku tabel: natural join, join, using, using on

Bazy danych
0
Tabele: pracownicy pracownik_id imie nazwisko stanowisko_id kierownik_id stanowiska stanowisko_id nazwa_stanowiska kierownik_id lokalizacja Zadanie 1 Przygotuj raport o wszystkich pracownikach pracujących w firmie i  ich stanowiskach. Informacje o pracownikach i ich stanowiskach są umieszczone są w rożnych tabelach. Należy napisać zapytanie SQL pobierające dane z dwóch różnych tabel używając połączeń JOINS.…
Load More
Menu