Algorytmy
Algorytmy dla początkujących
Kurs „Algorytmy dla uczniów”, przedstawia algorytmy dla początkujących i został przygotowany jako wstęp do algorytmiki dla uczniów. Algorytmika Powyższy materiał pochodzi z pracy „Algorytmika dla uczniów”, którą wykonałam podczas studiów. Materiały te przez długi czas były dostępne na stronie republiki…
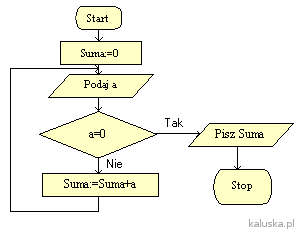
Sposoby zapisu algorytmu
Algorytmy powinny być tak przedstawiane, aby było możliwe ich jednoznaczne odczytanie i zastosowanie. Dlatego teraz poznasz różne sposoby zapisu algorytmów. Niektóre algorytmy można opisać słownie korzystając z języka potocznego. Jest to proste zwłaszcza wtedy, gdy algorytm jest prosty, a jego…
Algorytmy. Tablice dwuwymiarowe
Poniższy materiał to część cyklu „Algorytmy dla uczniów” Algorytmy obsługi tablic dwuwymiarowych Przykład tablicy dwuwymiarowej: Do poszczególnych elementów tablicy uzyskujemy dostęp poprzez podanie nazwy tablicy oraz w nawiasach kwadratowych wartość indeksu ( numer żądanego elementu). I tak w naszej tablicy…
Specyfikacja algorytmu, czyli specyfikacja problemu algorytmicznego
Poniższy materiał to część cyklu „Algorytmy dla uczniów” Wiemy już, co to są algorytmy i jak można je zapisywać. Potrafimy więc przetworzyć dane, by otrzymać poprawne wyniki. Dane … wyniki … czym one są? Specyfikacja algorytmu (specyfikacja zadania) Specyfikacja algorytmu…