PL/SQL. Rodzaje bloków
WSTĘP DO PL/SQL Rodzaje bloków PL/SQL: 1. bloki anomimowe (nienazwane) declared inline 2. bloki nazwane (podprogramy) Blok anonimowy Uruchamiamy program Oracle SQL Developer. Wpisujemy poniższy kod: BEGINDBMS_OUTPUT.PUT_LINE(’Hello World!’);END; By wykonać kod wciskamy przycisk Run Script (zielona strzałka z kartką) lub wciskamy…
SQL. Pobieranie danych z kilku tabel: natural join, join, using, using on
Tabele: pracownicy pracownik_id imie nazwisko stanowisko_id kierownik_id stanowiska stanowisko_id nazwa_stanowiska kierownik_id lokalizacja Zadanie 1 Przygotuj raport o wszystkich pracownikach pracujących w firmie i ich stanowiskach. Informacje o pracownikach i ich stanowiskach są umieszczone są w rożnych tabelach. Należy napisać zapytanie…
Algorytm Euklidesa
Poniższy materiał to część cyklu „Algorytmy dla uczniów” Algorytm Euklidesa czyli algorytm wyznaczania NWD – największego wspólnego dzielnika dwóch liczb całkowitych. Na początku wykonajmy proste zadanie. Zadanie:Wyznacz największy wspólny dzielnik dwóch liczb naturalnych: 12 , 18. Na początku wypiszmy wszystkie…
Algorytmy. Przykłady i zadania
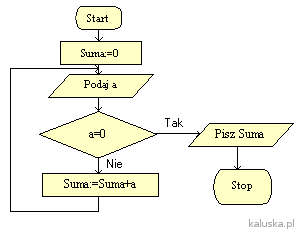
Poniższy materiał to część cyklu „Algorytmy dla uczniów, czyli algorytmy dla początkujących”. Poznałeś już kilka przykładów algorytmów. Przeanalizuj je ponownie, a następnie przejdź do wykonywania poniższych zadań. Poniżej przedstawiam kilka przykładów algorytmów. Zachęcam Cię, abyś po przeczytaniu treści zadania zastanowił…
Rodzaje algorytmów
Artykuł ten jest częścią cyklu „Algorytmy dla uczniów”, czyli algorytmy dla początkujących. Jakie rodzaje algorytmów możemy wyróżnić? Rodzaje algorytmów: algorytmy liniowe, czyli algorytmy sekwencyjne algorytmy warunkowe, czyli algorytmy z rozgałęzieniami algorytmy iteracyjne, czyli algorytmy z pętlą, inaczej algorytmy cykliczne algorytmy…
Algorytmy dla początkujących
Kurs „Algorytmy dla uczniów”, przedstawia algorytmy dla początkujących i został przygotowany jako wstęp do algorytmiki dla uczniów. Algorytmika Powyższy materiał pochodzi z pracy „Algorytmika dla uczniów”, którą wykonałam podczas studiów. Materiały te przez długi czas były dostępne na stronie republiki…
Sposoby zapisu algorytmu
Algorytmy powinny być tak przedstawiane, aby było możliwe ich jednoznaczne odczytanie i zastosowanie. Dlatego teraz poznasz różne sposoby zapisu algorytmów. Niektóre algorytmy można opisać słownie korzystając z języka potocznego. Jest to proste zwłaszcza wtedy, gdy algorytm jest prosty, a jego…
Algorytmy. Tablice dwuwymiarowe
Poniższy materiał to część cyklu „Algorytmy dla uczniów” Algorytmy obsługi tablic dwuwymiarowych Przykład tablicy dwuwymiarowej: Do poszczególnych elementów tablicy uzyskujemy dostęp poprzez podanie nazwy tablicy oraz w nawiasach kwadratowych wartość indeksu ( numer żądanego elementu). I tak w naszej tablicy…
Specyfikacja algorytmu, czyli specyfikacja problemu algorytmicznego
Poniższy materiał to część cyklu „Algorytmy dla uczniów” Wiemy już, co to są algorytmy i jak można je zapisywać. Potrafimy więc przetworzyć dane, by otrzymać poprawne wyniki. Dane … wyniki … czym one są? Specyfikacja algorytmu (specyfikacja zadania) Specyfikacja algorytmu…
Kurs SQL na przykładzie Oracle: zaczynamy
Aby nauczyć się SQL musimy go używać. Ja proponuję szybki start przy pomocy Virtualnej Maszyny. Instalujemy program Virtual Box i na nim gotową maszynę wirtualną przygotowaną przez Oracle: Oracle VM VirtualBox Oracle DB Developer VM (DeveloperDaysVM.ova – ponad 7GB) Oba narzędzia…