Co to jest algorytm. Podstawy algorytmów
Co to jest algorytm ? Na lekcjach matematyki czy fizyki często słyszymy zdanie „rozwiąż zadanie”. Większość tych zadań rozwiązujemy według pewnych schematów. Najpierw wypisujemy dane i zastanawiamy się do jakiego celu dążymy, a więc jaki ma być wynik. Następnie wypisujemy…
Schematy blokowe algorytmów
Schemat blokowy to graficzny sposób przedstawienia algorytmu. Schemat składa się z bloków oraz połączeń między nimi. Bloki to figury geometryczne, w których zapisywane są działania, operacje algorytmu. Kolejność wykonywania operacji wskazują połączenia między blokami. Do tej pory (patrz lekcja 1)…
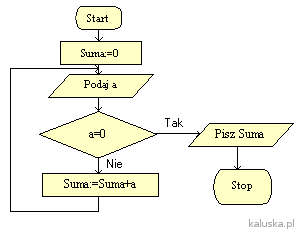
Algorytmy: ciągi liczb. Schematy blokowe algorytmów
Poniższy artykuł dotyczący przykładów algorytmów bazujących na ciągach liczb to część cyklu „Algorytmy dla uczniów”, czyli algorytmy dla początkujących Ciągi w algorytmach. Przykłady schematów blokowych Przykład 1Dany jest ciąg liczb o nieznanej długości. Ostatnia liczba w ciągu równa się zero.…
Algorytmy sortowania
Poniższy materiał to część cyklu „Algorytmy dla uczniów”, czyli algorytmy dla początkujących. Zapraszam do zapoznania się z całością cyklu. ALGORYTMY SORTOWANIA (PORZĄDKOWANIA) Sortowanie (porządkowanie) – proces ustawienia zbioru obiektów w określonym porządku Metody sortowania: przez zamianę (sortowanie bąbelkowe) przez wybieranie przez…
Algorytm. Gra Papier Kamień Nożyce
Poniższy materiał to część cyklu „Algorytmy dla uczniów” Grę „Papier Kamień Nożyce” znają chyba wszyscy. Tym razem naszym zadaniem jest stworzenie algorytmu wskazującego zwycięzcę tej gry. Zakładamy, że w grze uczestniczą dwaj gracze. Każdy z graczy może wybrać (pokazać) jedną z…
Algorytm. Obliczanie pola trójkąta
Poniższy materiał to część cyklu „Algorytmy dla uczniów” Stworzymy teraz algorytm obliczający pole trójkąta. Rozpoczniemy od zapisania specyfikacji problemu. Specyfikacja algorytmu obliczającego pole trójkąta Problem: Obliczanie pola trójkąta. Dane: a, b, c – trzy dowolne liczby Wynik: Jeśli liczby a, b,…
Algorytmy. Tablice jednowymiarowe
Poniższy materiał jest częścią cyklu „Algorytmy dla uczniów”, czyli algorytmy dla początkujących. W ramach cyklu powstało kilka lekcji dla uczniów, zapraszam do zapoznania się z nimi. W tej części zajmiemy się algorytmami dotyczącymi tablic. ALGORYTMY OBSŁUGI TABLIC Tablicą nazywamy złożoną…
Algorytm Euklidesa
Poniższy materiał to część cyklu „Algorytmy dla uczniów” Algorytm Euklidesa czyli algorytm wyznaczania NWD – największego wspólnego dzielnika dwóch liczb całkowitych. Na początku wykonajmy proste zadanie. Zadanie:Wyznacz największy wspólny dzielnik dwóch liczb naturalnych: 12 , 18. Na początku wypiszmy wszystkie…
Algorytmy. Przykłady i zadania
Poniższy materiał to część cyklu „Algorytmy dla uczniów, czyli algorytmy dla początkujących”. Poznałeś już kilka przykładów algorytmów. Przeanalizuj je ponownie, a następnie przejdź do wykonywania poniższych zadań. Poniżej przedstawiam kilka przykładów algorytmów. Zachęcam Cię, abyś po przeczytaniu treści zadania zastanowił…
Rodzaje algorytmów
Artykuł ten jest częścią cyklu „Algorytmy dla uczniów”, czyli algorytmy dla początkujących. Jakie rodzaje algorytmów możemy wyróżnić? Rodzaje algorytmów: algorytmy liniowe, czyli algorytmy sekwencyjne algorytmy warunkowe, czyli algorytmy z rozgałęzieniami algorytmy iteracyjne, czyli algorytmy z pętlą, inaczej algorytmy cykliczne algorytmy…