Schematy blokowe algorytmów

Schemat blokowy to graficzny sposób przedstawienia algorytmu. Schemat składa się z bloków oraz połączeń między nimi. Bloki to figury geometryczne, w których zapisywane są działania, operacje algorytmu. Kolejność wykonywania operacji wskazują połączenia między blokami.

Do tej pory (patrz lekcja 1) do opisu algorytmów używaliśmy języka potocznego. Taki sposób świetnie się sprawdza gdy algorytmy są proste, czy po prostu ma wykonywać je człowiek. W przypadku algorytmów bardziej skomplikowanych czy też algorytmów, które wykonywać ma komputer –  ten zapis będzie nieczytelny, zwyczajnie nie sprawdzi się. Dlatego teraz poznamy nową, bardziej przejrzystą metodę – schematy blokowe.

Elementy schematu blokowego

W schemacie blokowym poszczególne operacje przedstawione są za pomocą odpowiednio połączonych bloków (klocków, skrzynek).  W literaturze informatycznej przyjęto pewne standardowe oznaczenia poszczególnych działań i te będziemy stosować.  Można również używać innych oznaczeń. Muszą one jednak być takie same dla określonego typu operacji.

Przykładowe bloki

Symbol graficzny	Nazwa bloku	Funkcja	Opis
	Blok graniczny	Początek algorytmu lub koniec	Ma kształt owalu. Ze skrzynki START wychodzi tylko jedno połączenie, skrzynka STOP nie ma połączenia wychodzącego
	Blok operacyjny	Wykonywanie różnych działań, np. działanie sumowania	Ma kształt prostokąta
	Blok wejścia / wyjścia	Wprowadzanie (czytanie) danych lub wyprowadzanie (drukowanie, pisanie) wyników	Jest równoległobokiem, wchodzi i wychodzi z niej jedno połączenie
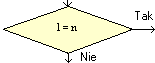	Blok warunkowy	Sprawdzanie warunku, np. czy N > 0	Ma kształt rombu. Ze skrzynki wychodzą tylko dwa połączenia: jedno oznaczone TAK, a drugie NIE

Dzięki wykorzystaniu różnych rodzajów bloków tworzymy schemat na którym można przedstawić działanie algorytmu.

Bloki składające się na algorytm muszą zostać ze sobą połączone. Połączenia mają postać linii ze strzałkami, które wskazują kolejność ich wykonywania.

Połączenia określają kolejność i sposób wykonywania operacji realizujących dany algorytm.

ZASADY BUDOWANIA SCHEMATU BLOKOWEGO

• Każda operacja powinna być umieszczona w skrzynce (bloku).
• Schemat powinien posiadać tylko jedną skrzynkę „Start” i przynajmniej jedną skrzynkę „Stop”.
• Skrzynki powinny być ze sobą połączone.
• Ze skrzynki powinno wychodzić jedno połączenie; wyjątek stanowią skrzynki „Stop” (z której nie wychodzą już żadne połączenia) oraz „warunkowa” (z której wychodzą dwa połączenia opisane Tak i Nie – w zależności od tego czy warunek jest spełniony czy też nie; można wyjść jedną z dwóch dróg).

ALGORYTMY WARUNKOWE

Przypomnij: co to jest instrukcja warunkowa ?
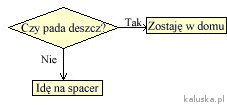
Z sytuacjami warunkowymi stykamy się w każdej dziedzinie życia codziennego. Na pytanie „Czy pada deszcz ?” odpowiedź może brzmieć „tak” lub „nie”. W zależności od tego, czy warunek jest spełniony, czy nie, wybieramy inne rozwiązanie.

Przykład sytuacji warunkowej:

Algorytm warunkowy

Przykład 1. Schemat algorytmu warunkowego
Podaj przykłady sytuacji warunkowych. Przedstaw je graficznie.

Wiesz już, że z sytuacją warunkową mamy do czynienia wówczas, gdy wynik lub dalsze działanie zależy od spełnienia warunku. Na schemacie blokowym sytuacje warunkowe realizujemy przez skrzynkę (blok) warunkową. Jak dotąd rozważane przez nas algorytmy przedstawiały problemy z życia. Teraz zajmiemy się rozwiązywaniem prostych zadań obliczeniowych, przy czym algorytm opracowany dla każdego z nich będzie miał postać schematu blokowego.

W skrzynce wpisujemy warunek logiczny, stosując znaki „=” równy,”<>” różny, „<” mniejszy, „>” większy,”<=” mniejszy lub równy, „>=” większy lub równy, np: (a > 5) lub (a <= 20), (a < 5)OR (a <= 20)
Z systemami warunkowymi spotykamy się m.in. w matematyce i fizyce, wtedy gdy wykonywanie działań jest uzależnione od warunku, jakie muszą spełniać liczby, np. mają być nieujemne albo parzyste.

Przykład 2. Schemat algorytmu warunkowego
Przestaw schemat blokowy algorytmu obliczania wartości bezwzględnej.

Najpierw oczywiście musimy wiedzieć co to jest wartość bezwzględna. Bez tej informacji nie jesteśmy w stanie napisać żadnego algorytmu (narysować schematu blokowego, czy też napisać programu).

Wartością bezwzględną liczby nieujemnej jest ta sama liczba, a wartością bezwzględną liczby ujemnej jest liczba do niej przeciwna.

Np wartość bezwzględna liczby 5, to liczba 5.
Wartość bezględna liczby -5, to liczba 5.
Wartość bezwzględna liczby 0, to 0.
W schemacie więc musimy użyć jakiejś skrzynki, która pozwoli nam na sprawdzenie tego warunku. Potrzebna jest więc nam skrzynka warunkowa. Umieścimy w niej napis „czy liczba >=0?”. Oznacza on: „czy liczba jest większa lub równa zero”.

Algorytm – schemat blokowy, wartość bezwzględna
Zadanie do samodzielnego wykonania
Wprowadź dwie liczby a i b. Przedstaw w postaci ciągu kroków i graficznie algorytm porównania tych liczb i wyprowadzania na wyjściu większej z nich. W przypadku liczb równych wyprowadź napis „liczby równe”.

ALGORYTMY ITERACYJNE

Przypomnij : co to są instrukcje iteracyjne ?
Czasami trzeba wykonać te same operacje na wielu liczbach. W takich przypadkach nie jest konieczne wielokrotne opisywanie działań lub rysowanie takich samych skrzynek. Stosujemy wówczas iterację. Mówimy także, że działania te wykonywane są w pętli. Liczba powtórzeń tych działań może być z góry określona lub zależeć od spełnienia warunku. Iteracja to najczęściej spotykana technika algorytmiczna.

Iteracja to technika algorytmiczna polegająca na wykonaniu tej samej instrukcji dla n zmiennych.
Iteracja oszczędza czas programisty, który ten musiałby spędzić wpisując instrukcję n razy, zależnie od liczby zmiennych. Liczba powtórzeń w iteracji jest zwykle z góry określona lub zależy od spełnienia określonego warunku.

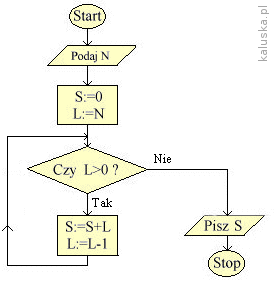
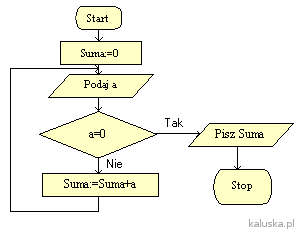
Przykład Analiza schematu algorytmu.
Przeanalizuj poniższy schemat blokowy i odpowiedz na pytania:

Jakie są dane wejściowe do zadania i jakich użyto zmiennych pomocniczych?
Jaki cel chcesz osiągnąć (wynik)?
Jaki algorytm zastosowano w operacji dodawania liczb ?
W którym miejscu wykonywane są dzivałania w pętli ?
Które operacje powtarzają się wielokrotnie ?
Co określa liczbę powtórzeń ?
Kiedy kończy się działanie w pętli ?
Iteracja

W analizowanym algorytmie występuje przypisanie typu S:=S + L. Oznacza ono przypisanie zmiennej „s” (sumie) poprzedniej wartości pamiętanej w zmiennej „s” (poprzedniej sumie) zwiększonej o wartość pamiętaną w zmiennej „l” (kolejną liczbę) – w ten sposób powtarzanie operacji przypisania, realizowane jest dodawanie kolejnych liczb naturalnych. Przypisania l:=l-1 ma tu bardzo istotne znaczenie. Jest to tzw. licznik, w którym następuje obliczanie, ile zostało jeszcze powtórzeń do wykonania. W tym algorytmie liczba powtórzeń została określona na początku instrukcją l:=n.

Gdyby nie umieszczono tego działania nastąpiło by tzw. zapętlenie algorytmu, czyli po sprawdzeniu warunku l>0 działanie w schemacie przebiegałoby zawsze drogą TAK. W realizacji algorytmów iteracyjnych ważne jest prawidłowe określenie sposobu zakończenia działań. Można to zrobić za pomocą licznika, który odlicza kolejne kroki iteracji (liczbę powtórzeń).


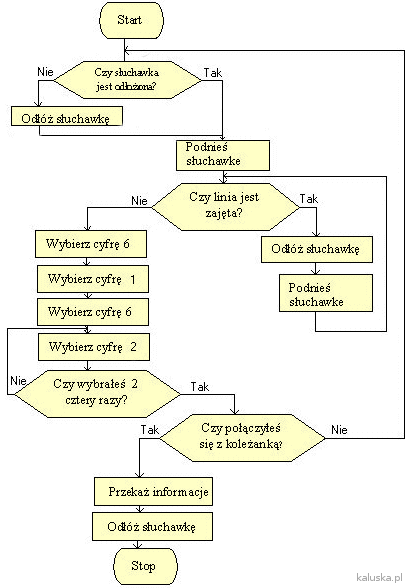
Przykład Schemat blokowy, algorytm z życia codziennego
Narysuj schemat blokowy algorytmu telefonicznego zaproszenia koleżanki w wersji pierwszej

Aplet Java. Schemat blokowy algorytmu z życia codziennego. Algorytm liniowy
Przykład Schemat blokowy, algorytm z życia codziennego
Narysuj schemat blokowy algorytmu telefonicznego zaproszenia koleżanki w wersji drugiej

Aplet Java. Schemat blokowy algorytmu z życia codziennego. Algorytm warunkowy
Przykład Schemat blokowy, algorytm z życia codziennego
Narysuj schemat blokowy algorytmu telefonicznego zaproszenia koleżanki w wersji piątej

Schemat blokowy, algorytm warunkowy iteracyjny (technika algorytmiczna. z życia codziennego).

Podsumowanie

Sposób rozwiązania zadania, czyli algorytm, można podać w kilku punktach. Mówimy wówczas, że algorytm jest opisany za pomocą listy kroków (ciągu kroków). Zapis taki polega na podaniu kolejnych wykonywanych operacji, składających się na całe rozwiązanie.

Algorytm można przedstawić również w postaci graficznej, za pomocą schematu blokowego. Schemat blokowy to graficzne przedstawienie ciągu kroków algorytmu, często stosowane jako ideowy rysunek poprzedzający tworzenie programu. Sposób i kolejność działań programu określane są przez wzajemny układ i sposób łączenia bloków (skrzynek) ze sobą. Każde działanie (krok) ma w schemacie blokowym swoje standardowe oznaczenie (patrz tabela wyżej).

Graficzne przedstawienie algorytmu to schemat blokowy. Ale nie tylko. Pamiętajmy również o drzewach, to kolejny ze sposobów na graficzny zapis algorytmu.

Ten artykuł jest częścią cyklu „Algorytmy dla uczniów”. Cały kurs zawierający materiały dotyczące algorytmów dla początkujących zawiera:

Lekcja 1: Co to jest algorytm? Podstawy algorytmów
Lekcja 2:  Sposoby zapisu algorytmów
Lekcja 3: Rodzaje algorytmów
Lekcja 4: Schematy blokowe algorytmów
Lekcja 5: Specyfikacja algorytmu. Specyfikacja problemu algorytmicznego
Lekcja 6: Algorytmy Przykłady i zadania 
Lekcja 6.1: Algorytmy. Przykłady i zadania.  Obliczanie pola trójkąta
Lekcja 6.2:  Algorytmy. Przykłady. Algorytm Euklidesa
Lekcja 6.3: Algorytm. Gra Kamień Papier Nożyce
Lekcja 7. Przykłady schematów blokowych. Ciągi liczb
Lekcja 8. Sortowanie – algorytmy sortowania
Lekcja 9: Algorytmy. Tablice jednowymiarowe
Lekcja 10. Algorytmy. Tablice dwuwymiarowe